SekaiCTF 2023

Hello all!
I have recently played SekaiCTF 2023.
Which was happened from Fri, 25 Aug. 2023, 21:30 IST to Sun, 27 Aug. 2023, 21:30 IST.

Here is the challenge from the category of Professional Programming & Coding (PPC)

Wiki Game #

Welcome to Project SEKAI Online Judge!

Author: sahuang

❖ Note : Time limit is 5 seconds. There is rate limiting and you can only submit once every 30 seconds. For simplicity, sample input 1.in is given in this challenge.

Server:   http://algo-server.chals.sekai.team

Files:
Wiki_Game.pdf
1.in

Problem Statement #

The Wiki Game is a hypertextual game designed to work specifically with Wikipedia. Player starts on some randomly selected article, and must navigate to another pre-selected target article solely by clicking links within each article. The goal is to arriveat the target article in the fewest clicks. According to Six degrees of Wikipedia, you can almost always complete the game in 6 clicks.

The Wikipedia database can be modelled as an unweighted, directed graph where each article corresponds to a vertex. It is important to note that the graph can contain cycles. Your goal is to efficiently determine whether it is possible to navigate from the source article to the target article within a maximum path length of 6.

Input #

The first line of input contains an integer T (1 ≤ T ≤ 20), the number of test cases. In each test case, the first line contains two space-separated integers n (2 ≤ n ≤ 1,000) and
m (1 ≤ m ≤ 4,000),the number of vertices and edges respectively. The next m lines describe the graph. The ith line contains two space-separated integers ui, vi (0 ≤ ui ≠ vi< n), meaning there exists a path from ui to vi . The last line contains two space-separated integers src, dst (0 ≤ src ≠ dst < n), the source and target vertices.

Output #

Output should have T lines. Each line prints YES if there exists a path from src to dst within a path length of 6, or NO otherwise. Remember to print them in upper-case.

Explanation #

In the first test case, there exists a path 0 → 1 → 2 → 3 → 4 → 5 → 6 of length 6, so the answer is YES. In the second test case, there is no path from 0 to 9 so the answer is NO. There is a path of length 3 from 9 to 0, but the graph is directed so it does not count.

To meet the time limit of 5 seconds and optimize the solution further, I used a breadth-first search (BFS) approach to find a path within a maximum of 6 steps. I thought BFS is a better choice for this scenario as it explores the graph level by level, ensuring that we can find the shortest path first.

Here’s the Python code using BFS:

CODE:

#!/usr/bin/env python3

def is_possible_to_reach(graph, src, dst):
    visited = [False] * len(graph)
    queue = [(src, 0)]

    while queue:
        node, depth = queue.pop(0)
        if node == dst:
            return True

        if depth >= 6:
            continue

        visited[node] = True

        for neighbor in graph[node]:
            if not visited[neighbor]:
                queue.append((neighbor, depth + 1))

    return False

def main():
    T = int(input())
    for _ in range(T):
        n, m = map(int, input().split())
        graph = [[] for _ in range(n)]

        for _ in range(m):
            u, v = map(int, input().split())
            graph[u].append(v)

        src, dst = map(int, input().split())

        if is_possible_to_reach(graph, src, dst):
            print("YES")
        else:
            print("NO")

if __name__ == "__main__":
    main()

This code should provide a faster solution using BFS, which is well-suited for finding paths in graphs. It will also handle the given time limit and rate limiting constraints more effectively.

Finally I got the flag,

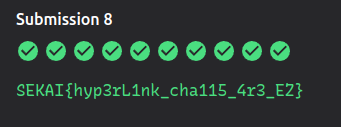
Flag : SEKAI{hyp3rL1nk_cha115_4r3_EZ}